时间序列(二):时间序列平稳性检测
时间序列系列文章:
时间序列(一):时间序列数据与时间序列预测模型
时间序列(二):时间序列平稳性检测
时间序列(三):ARIMA模型实战
在上一篇文章时间序列(一):时间序列数据与时间序列预测模型中我们介绍了时间序列及一些时间序列预测模型。我们可以看到在进行预测时有一些模型表现较好,而另一些模型的预测结果却不尽人意。这是因为不同的时间序列模型对原始数据的要求是不同的,例如之前提到的ARIMA模型,要求时间序列数据平稳,否则得出的预测结果就会相差较大。本篇文章我们介绍时间序列的平稳性、随机性检验及相关时间序列数据处理方法。
时间序列的平稳性、随机性检验
在拿到时间序列数据后,首先要对数据的随机性和平稳性进行检测, 这两个检测是时间序列预测的重要部分。根据不同检测结果需要采取不同的分析方法。
为什么时间序列要求平稳性呢?平稳性就是要求由样本拟合出的曲线在未来一段时间内仍然能够以现有的形态和趋势发展下去,这样预测结果才会有意义。
对于平稳声序列, 它的均值和方差是常数, 现已有一套非常成熟的平稳序列的建模方法。 通常是建立一个线性模型来拟合该序列的发展 借此提取该序列的有用信息。
对于非平稳序列, 由于它的均值和方差不稳定, 处理方法一般是将其转变为平稳序列,这样就可以应用有关平稳时间序列的分析方法, 如建立 ARIMA模型来进行相应的研究,或者分解趋势与季节性等并根据情况应用指数平滑模型等。
对于纯随机序列, 又称为白噪声序列, 序列的各项之间没有任何相关关系, 序列在进行完全无序的随机波动, 可以终止对该序列的分析。 白噪声序列是没有信息可提取的平稳序列。
在讲解平稳性和随机性的定义之前,我们先介绍一下时间序列中常用的几个特征统计量。
时间序列的特征统计量
对于一个时间序列任意时刻的序列值 { X t , t ∈ T } \left\{ X _ { t } , t \in T \right\} {Xt,t∈T},任意时刻的序列值 X t X _ { t } Xt都是一个随机变量,记其分布函数为 F t ( x ) F _ { t } ( x ) Ft(x),则其特征统计量均值、方差、自协方差函数、自相关系数的定义分别如下:
均值: 表示时间序列在各个时刻取值的平均值,其定义如下:
μ
t
=
E
X
t
=
∫
−
∞
∞
x
d
F
t
(
x
)
\mu _ { t } = E X _ { t } = \int _ { - \infty } ^ { \infty } x \mathrm { d } F _ { t } ( x )
μt=EXt=∫−∞∞xdFt(x)
方差: 表示时间序列在各个时刻围绕其均值波动的平均程度,其定义如下:
σ
t
2
=
D
X
t
=
E
(
X
t
−
μ
t
)
2
=
∫
−
∞
∞
(
x
−
μ
t
)
2
d
F
t
(
x
)
\sigma _ { t } ^ { 2 } = D X _ { t } = E \left( X _ { t } - \mu _ { t } \right) ^ { 2 } = \int _ { - \infty } ^ { \infty } \left( x - \mu _ { t } \right) ^ { 2 } \mathrm { d } F _ { t } ( x )
σt2=DXt=E(Xt−μt)2=∫−∞∞(x−μt)2dFt(x)
自协方差 : 表示时间序列任意两个时刻直接的相关性,任取
t
,
s
∈
T
t , s \in T
t,s∈T,则其定义如下:
γ
(
t
,
s
)
=
E
[
(
X
t
−
μ
t
)
(
X
s
−
μ
s
)
]
\gamma ( t , s ) = E \left[ \left( X _ { t } - \mu _ { t } \right) \left( X _ { s } - \mu _ { s } \right) \right]
γ(t,s)=E[(Xt−μt)(Xs−μs)]
自相关系数: 同自协方差函数,其定义如下:
ρ ( t , s ) = γ ( t , s ) D X t ⋅ D X s \rho ( t , s ) = \frac { \gamma ( t , s ) } { \sqrt { D X _ { t } \cdot D X _ { s } } } ρ(t,s)=DXt⋅DXsγ(t,s)
平稳时间序列的定义与检验
平稳时间序列的定义
平稳时间序列按照限定条件的严格程度可以分为以下两种类型:
严平稳时间序列: 指时间序列的所有统计性质不会随着时间的推移而发生变化,即其联合概率分布在任何时间间隔都是相同的。设 { X t } \left\{ X _ { t } \right\} {Xt}为一时间序列,对任意的正整数 m m m,任取 t 1 , t 2 , ⋯ , t m ∈ T t _ { 1 } , t _ { 2 } , \cdots , t _ { m } \in T t1,t2,⋯,tm∈T,对任意整数 τ \tau τ,有:
F t 1 , t 2 , ⋯ , t m ( x 1 , x 2 , ⋯ , x m ) = F t 1 + τ , t 2 + τ , ⋯ , t m + τ ( x 1 , x 2 , ⋯ , x m ) F _ { t _ { 1 } , t _ { 2 } , \cdots , t _ { m } } \left( x _ { 1 } , x _ { 2 } , \cdots , x _ { m } \right) = F _ { t _ { 1 + \tau } , t _ { 2 + \tau } , \cdots , t _ { m + \tau } } \left( x _ { 1 } , x _ { 2 } , \cdots , x _ { m } \right) Ft1,t2,⋯,tm(x1,x2,⋯,xm)=Ft1+τ,t2+τ,⋯,tm+τ(x1,x2,⋯,xm)
则称时间序列 { X t } \left\{ X _ { t } \right\} {Xt}为严平稳时间序列。
宽平稳时间序列: 宽平稳时间序列则认为只要时间序列的低阶距(二阶)平稳,则该时间序列近似平稳。如果时间序列 { X t } \left\{ X _ { t } \right\} {Xt}满足以下三个条件:
- 任取 t ∈ T t \in T t∈T,有 E X t 2 < ∞ EX _ { t }^ { 2 } <∞ EXt2<∞
- 任取 t ∈ T t \in T t∈T,有 E X t = μ E X _ { t } = \mu EXt=μ,其中 μ \mu μ为常数;
- 任取 t , s , k ∈ T t , s , k \in T t,s,k∈T, k + s − t ∈ T k + s - t \in T k+s−t∈T,有 γ ( t , s ) = γ ( k , k + s − t ) \gamma ( t , s ) = \gamma ( k , k + s - t ) γ(t,s)=γ(k,k+s−t)
在现实生活中,时间序列是很难满足严平稳时间序列的要求的,因此,一般所讲的平稳时间序列在默认情况下都是指宽平稳时间序列。根据宽平稳时间序列的条件,我们可以容易得到宽平稳时间序列所具有的性质:
- 均值为常数,即: E X t = μ , ∀ t ∈ T E X _ { t } = \mu , \quad \forall t \in T EXt=μ,∀t∈T
- 方差也为均值,即: D X t = γ ( t , t ) = γ ( 0 ) , ∀ t ∈ T D X _ { t } = \gamma ( t , t ) = \gamma ( 0 ) , \quad \forall t \in T DXt=γ(t,t)=γ(0),∀t∈T
- 自协方差函数和自相关系数只依赖于时间的平移长度,而与时间的起点无关。即:
γ
(
t
,
s
)
=
γ
(
k
,
k
+
s
−
t
)
,
∀
t
,
s
,
k
∈
T
\gamma ( t , s ) = \gamma ( k , k + s - t ) , \quad \forall t , s , k \in T
γ(t,s)=γ(k,k+s−t),∀t,s,k∈T
因此,可以记 γ ( k ) \gamma ( k ) γ(k)为时间序列${ X _ { t } $的延迟k自协方差函数。
由于平稳时间序列具有这些优良性质,因此,对于一个平稳时间序列来说,其待估计的参数量就变得少了很多,因为他们的均值、方差都是一样的,因此,可以利用全部的样本来估计总体的均值和方差,即:
μ
^
=
x
‾
=
∑
i
=
1
n
x
i
n
γ
^
(
0
)
=
∑
t
=
1
n
(
x
t
−
x
‾
)
2
n
−
1
\widehat { \mu } = \overline { x } = \frac { \sum _ { i = 1 } ^ { n } x _ { i } } { n } \\ \widehat { \gamma } ( 0 ) = \frac { \sum _ { t = 1 } ^ { n } \left( x _ { t } - \overline { x } \right) ^ { 2 } } { n - 1 }
μ
=x=n∑i=1nxiγ
(0)=n−1∑t=1n(xt−x)2
这也是为什么说当拿到一个时间序列后,需要对其进行平稳性检验。
平稳时间序列的检验
那么,当拿到一个时间序列后,应该如何对其进行平稳性的检验呢?目前,对时间序列的平稳性检验主要有两种方法,一种是图检法,即根据时序图和自相关图进行直观判断,另一种是构造检验统计量的方法,有单位根检验法等方法。
图检法
对于图检法,我们一般绘制时间序列的时序图,考虑以下三个图形:
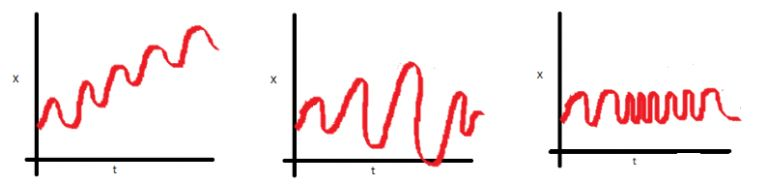
在第一幅图中,我们可以清楚地看到,均值随时间而变化(增加),呈现上升的趋势。因此,这是一个非平稳序列。平稳序列不应该呈现出随时间变化的趋势。
第二幅图显然看不到序列的趋势,但序列的变化是一个时间的函数。正如前面提到的,平稳序列的方差必须是一个常数。
再来看第三幅图,随着时间的增加,序列传播后变得更近,这意味着协方差是时间的函数。
所以上述三个例子均是非平稳时间序列.
再看下面的时序图:
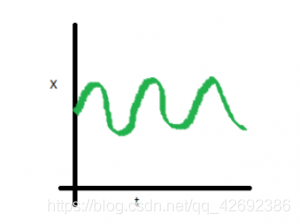
在这张图中,均值、方差和协方差都是常数,这就是平稳时间序列
另一方面,我们也可以通过自相关图来进行检验,对于平稳时间序列,其自相关图一般随着阶数的递增,自相关系统会迅速衰减至0附近,而非平稳时间序列则可能存在先减后增或者周期性波动等变动。如下图所示,该时间序列随着阶数的递增,自相关系数先减后增,因此,可以判断该时间序列不是平稳时间序列。
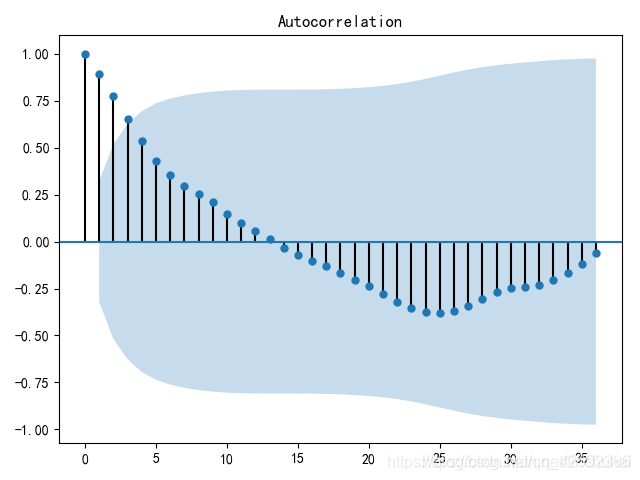
统计检验
可以利用统计检验来代替目视检验:比如单位根平稳检验。单位根表名给定序列的统计特性(均值,方差和协方差)不是时间的常数,这是平稳时间序列的先决条件。下面是它的数学解释:
假设我们有一个时间序列:
y
t
=
a
∗
y
t
−
1
+
ε
t
y_t=a*y_{t-1 }+ε_t
yt=a∗yt−1+εt
其中
y
t
y_t
yt是t时刻的数据值,
ε
t
ε_t
εt 是误差项。
仙子我们需要利用
y
t
−
1
y_{t-1 }
yt−1的值来计算
y
t
y_t
yt,即:
y
t
−
1
=
a
∗
y
t
−
2
+
ε
t
−
1
y_{t-1}=a*y_{t-2}+ε_{t-1}
yt−1=a∗yt−2+εt−1
如果利用所有的观察值,
y
t
y_{t}
yt的值将是:
y
t
=
a
n
∗
y
t
−
n
+
∑
ε
t
−
i
∗
a
i
y_{t}=a^n*y_{t-n}+ \sumε_{t-i}*a^i
yt=an∗yt−n+∑εt−i∗ai
假设在上述方程中a的值为1(单位),则预测值将等于 y t − n y_{t-n} yt−n 和从 t − n t-n t−n到 t t t的所有误差之和,这意味着方差将随着时间的推移而增大,这就是时间序列中的单位根。众所周知,平稳时间序列的方差不能是时间的函数。单元根检验通过检查a=1的值来检查序列中是否存在单位根。以下是两个最常用的单位根平稳检测方法:
ADF(增补迪基-福勒)检验
迪基-福勒(Dickey Fuller)检验是最流行的统计检验方法之一,可以用它来确定序列中单位根的存在,从而帮助判断序列是否是平稳。ADF检验是对DF检验的扩展。这一检验的原假设与备选假设如下:
- 原假设: 序列有一个单位根(序列非平稳)
- 备选假设: 该序列没有单位根。(序列平稳)
单位根是什么呢?当一个自回归过程中: y t = b y t − 1 + a + ϵ t y_{t} = by_{t-1} + a + \epsilon _{t} yt=byt−1+a+ϵt,如果滞后项系数b为1,就称为单位根。当单位根存在时,自变量和因变量之间的关系具有欺骗性,因为残差序列的任何误差都不会随着样本量(即时期数)增大而衰减,也就是说模型中的残差的影响是永久的。这种回归又称作伪回归。如果单位根存在,这个过程就是一个随机漫步(random walk)。ADF检验就是判断序列是否存在单位根:如果序列平稳,就不存在单位根;否则,就会存在单位根.
在Python中使用ADF检验可以在statsmodels中使用adfuller函数。在下面的代码中我们加上标题与输出值对应的名称:
#定义ADF输出格式化函数
from statsmodels.tsa.stattools import adfuller
def adf_test(timeseries):
print ('ADF检验结果:')
dftest = adfuller(timeseries, autolag='AIC')
dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','Number of Lags Used','Number of Observations Used'])
for key,value in dftest[4].items():
dfoutput['Critical Value (%s)'%key] = value
print (dfoutput)
#对数据集使用ADF检验
adf_test(train['#Passengers'])
检验结果如下:
ADF检验结果:
Test Statistic 0.815369
p-value 0.991880
Number of Lags Used 13.000000
Number of Observations Used 130.000000
Critical Value (1%) -3.481682
Critical Value (5%) -2.884042
Critical Value (10%) -2.578770
dtype: float64
ADF的结果主要看以下两个方面:
- Test Statistic的值如果比Critical Value (5%)小则满足稳定性需求.
- p-value越低(理论上需要低于0.05)证明序列越稳定。
在上面的例子中,test statistic > Critical Value (5%) ,这意味着序列不是平稳的。同时p值为0.99,这证实了我们最初在目视检测中观察的结果。
随机性(白噪声)的定义与检验
随机性时间序列的定义
通过对时间序列进行平稳性检验后,我们可以将时间序列分为平稳时间序列和非平稳时间序列,对于非平稳时间序列,一般需要将其转化为平稳时间序列再进行分析,具体的转化方法随后再讲。而对于平稳时间序列,我们知道其有一个性质,即自协方差函数和自相关系数只依赖于时间间隔,而与起点无关,对于相同的时间间隔,其自协方差函数和自相关系数为一个常数,那么,就存在一种情况,当该常数为0时,照样满足平稳时间序列的条件,而此时序列之间的相关性则为0,即序列之间不相关,那么,这时我们的分析即可结束,因为对于一个毫无相关的序列,我们没法从中挖掘出可用的规律,此时的序列即为随机性时间序列,也称为白噪声序列。
对于时间序列
X
t
X _ { t }
Xt,如果满足:
- 任取 t ∈ T t \in T t∈T,有 E X t = μ E X _ { t } = \mu EXt=μ;
- 任取
t
,
s
∈
T
t , s \in T
t,s∈T,有
γ ( t , s ) = σ 2 ; t = s 0 ; t ≠ s \gamma ( t , s ) = \begin{array} { l l } { \sigma ^ { 2 }}; { t = s } \\ { 0 }; { t \neq s } \end{array} γ(t,s)=σ2;t=s0;t=s
则称该时间序列为纯随机序列或白噪声序列,简记为 X t ∼ W N ( μ , σ 2 ) X _ { t } \sim W N \left( \mu , \sigma ^ { 2 } \right) Xt∼WN(μ,σ2)。我们可以发现,其实白噪声序列的性质与平稳时间序列的性质一样,其均值和方差均为常数,只是自协方差函数或自相关系数为0,因此,该序列的任何两项之间不存在相关性,无法从中得到任何有用的信息,此时分析可以停止。
纯随机性(白噪声)检验
对于纯随机性序列,一般通过构建统计量的方法来检验。我们知道,白噪声序列除了0阶自相关系数外,即方差,其他阶的自相关系数应该均为0,因此,我们可以提出下面这样一个假设:
H 0 : ρ 1 = ρ 2 = ⋯ = ρ m = 0 , ∀ m ⩾ 1 H 1 : 至 少 存 在 某 个 ρ k ≠ 0 , ∀ m ⩾ 1 , k ⩽ m H _ { 0 } : \rho _ { 1 } = \rho _ { 2 } = \cdots = \rho _ { m } = 0 , \quad \forall m \geqslant 1\\ H _ { 1 } :至少存在某个\rho _ { k } \neq 0 , \quad \forall m \geqslant 1 , k \leqslant m H0:ρ1=ρ2=⋯=ρm=0,∀m⩾1H1:至少存在某个ρk=0,∀m⩾1,k⩽m
因此,围绕该假设,我们可以构建统计量进行检验,常用的统计量有Q统计量和LB统计量,其计算公式分别如下:
Q = n ∑ k = 1 m ρ ^ k 2 L B = n ( n + 2 ) ∑ k = 1 m ( ρ ^ k 2 n − k ) Q = n \sum _ { k = 1 } ^ { m } \widehat { \rho } _ { k } ^ { 2 }\\L B = n ( n + 2 ) \sum _ { k = 1 } ^ { m } \left( \frac { \widehat { \rho } _ { k } ^ { 2 } } { n - k } \right) Q=n∑k=1mρ k2LB=n(n+2)∑k=1m(n−kρ k2)
其中, n n n为序列的观察期数, m m m为指定延迟期数, k k k为延迟阶数,Box和Pierce证明这两个统计量均服从自由度为m mm的卡方分布,当统计量大于 χ 1 − α 2 ( m ) \chi _ { 1 - \alpha } ^ { 2 } ( m ) χ1−α2(m)或者P值小于 α α α 时,则认为可以拒绝原假设,即认为该序列是非随机序列
我们可以使用acorr_ljungbox函数进行数据的纯随机性检验.语法为:
acorr_ljungbox(x, lags=None, boxpierce=False) # 数据的纯随机性检验函数
lags:为延迟期数,如果为整数,则是包含在内的延迟期数,如果是一个列表或数组,那么所有时滞都包含在列表中最大的时滞中
boxpierce:为True时表示除开返回LB统计量还会返回Box和Pierce的Q统计量
返回值:
lbvalue:测试的统计量
pvalue:基于卡方分布的p统计量
bpvalue:((optionsal), float or array) – 基于 Box-Pierce 的检验的p统计量
bppvalue:((optional), float or array) – 基于卡方分布下的Box-Pierce检验的p统计量
代码实现:
from statsmodels.stats.diagnostic import acorr_ljungbox
acorr_ljungbox(train['#Passengers'])
输出检验结果中会返回两个值:
lbvalue: 测试的统计量 和 pvalue: 基于卡方分布的p统计量。如果p-value>0.05则可判断为白噪声序列
时间序列的平稳化
在熟悉了平稳性的概念及其不同的类型之后,接下来可以对序列进行平稳化操作。平稳化的方法有以下几种:
差分法
在该方法中,计算序列中连续项的差值。执行差分操作通常是为了消除均值的变化。从数学角度,差分可以写成:
y t = y t – y t − 1 y_t = y_t – y_{t-1} yt=yt–yt−1
其中 y t y_t yt 是t时刻的数值。相减数值之间的间隔数即为阶数。例如上述公式即为一阶差分。
我们可以直接相减对序列差分,并绘制出对应线图:
train['#Passengers_diff'] = train['#Passengers'] - train['#Passengers'].shift(1)
train['#Passengers_diff'].dropna().plot()
或者使用diff方法进行差分:
train['#Passengers_diff'] = train['#Passengers'].diff(1)#一阶差分
train['#Passengers_diff2'] = train['#Passengers_diff'].diff(1)#二阶差分
当数据存在季节性趋势时,我们可以利用季节性差分来消除季节性的不平稳因素。例如,星期一的观察值将与上星期一的观察值相减。从数学角度,它可以写成:
y t = y t – y t − n y_t = y_t – y_{t-n} yt=yt–yt−n
n=7
train['#Passengers_diff'] = train['#Passengers'] - train['#Passengers'].shift(n)
变换
变换用于对方差为非常数的序列进行平稳化。常用的变换方法包括幂变换、平方根变换和对数变换。
train['#Passengers_log'] = np.log(train['#Passengers'])
train['#Passengers_log_diff'] = train['#Passengers_log'] - train['#Passengers_log'].shift(1)
train['#Passengers_log_diff'].dropna().plot()
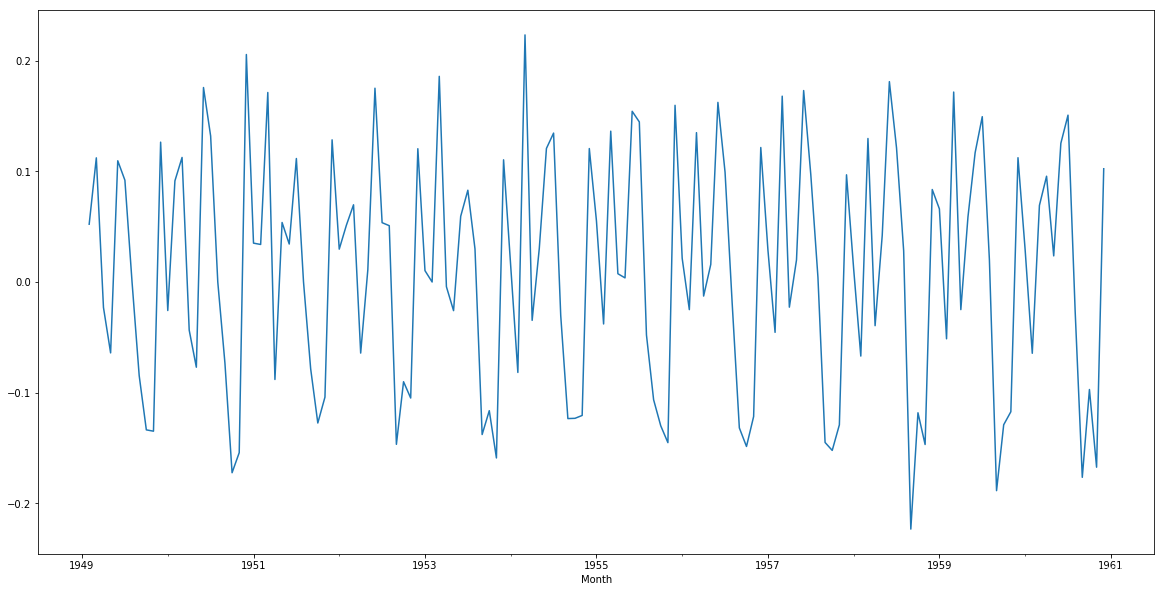
在上面的变化过程中,我们首先对原始数据取对数,主要有两个用处:(1)将指数增长转为线性增长(2)可以平稳序列的方差。随后进行差分从而消除趋势的影响使序列平稳。
分解
对于有明显趋势或者周期性的时间序列二,我们也可以对其进行分解。分解需要用到statsmodels.tsa.seasonal.seasonal_decompose函数,可以将时间序列的数据分解为趋势(trend),季节性(seasonality)和残差(residual)三部分。
from statsmodels.tsa.seasonal import seasonal_decompose
decomposition = seasonal_decompose(train['#Passengers']).plot()#画出分解后时序图
plt.show()
trend = decomposition.trend
seasonal = decomposition.seasonal
residual = decomposition.resid
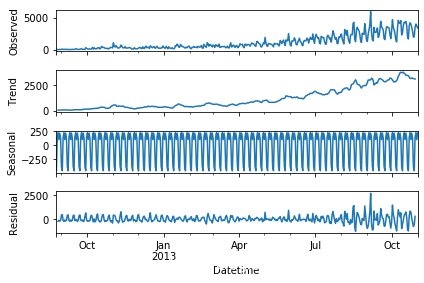
这样趋势和季节性,还有残差值都被分解出来,之后我们就可以计算残差值的稳定性,从而得到一个平稳的时间序列
参考文章:
https://www.biaodianfu.com/arima.html
