离散时间序列的傅里叶变换和基本性质
目录
1、由连续时间序列的傅里叶变换:
可以以此类推离散时间序列的傅里叶变换为
由于序列是离散的,所以求FT公式的时候用的累加;由于离散时间系统的FT是周期连续函数,且周期是2π(所以下面我们上下限选择的是+π),则可以直接用连续时间系统的FT公式带入。下面对离散时间系统的x(n)公式做一下验证:
至于这个2π周期,简要写一下:
其中M是整数
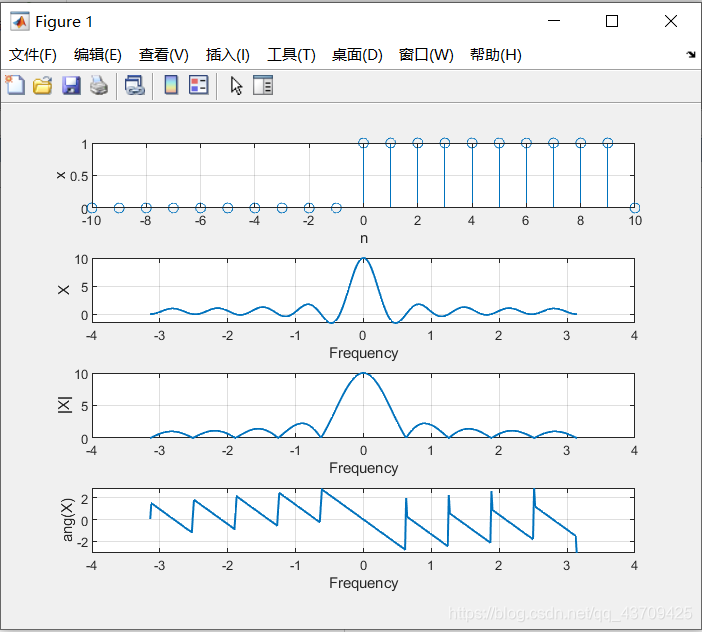
下面是一个具体实例,附加matlab代码:
n=-10:10;
x=[(n>=0)&(n<10)];
k=-200:200;
w=(pi/200)*k;
X=x*(exp(-j*pi/200)).^(n'*k);
magX=abs(X);
angX=angle(X);
subplot(4,1,1);
stem(n,x);
xlabel('n');
ylabel('x');
grid on;
subplot(4,1,2);
plot(w,X,'LineWidth',1);
xlabel('Frequency');
ylabel('X');
grid on;
subplot(4,1,3);
plot(w,magX,'LineWidth',1);
xlabel('Frequency');
ylabel('|X|');
grid on;
subplot(4,1,4);
plot(w,angX,'LineWidth',1);
xlabel('Frequency');
ylabel('ang(X)');
grid on;
2、DTFT的一些·常用性质
(1)时移性质
证明:
推导过程中使用了一步换元法:
(2)频移性质
证明:
3、序列的对称性(这个比较重要)
首先介绍两个概念:
共轭对称序列条件:
,记做
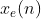
共轭反对称序列条件:
,记做
(1)实部与虚部的奇偶性
由共轭对称序列与共轭反对称序列的条件可知:
(1)若一个序列为共轭对称序列,那么
即实部为偶函数
即虚部为奇函数
(2)若一个序列是共轭反对称序列,那么
即实部是奇函数
即虚部是偶函数
(2)序列的表示
任何一个序列都可以由共轭对称序列和共轭反对称序列的和表示,即:
那么
因此,易得
(3)序列FT的对称性
首先推导三个比较重要的公式:
性质一:
序列x(n)的实部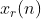 的FT具有共轭对称性;序列x(n)的
的FT具有共轭对称性;序列x(n)的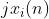 具有共轭反对称性,即:
具有共轭反对称性,即:
证明:
同理可得:
性质二:
序列x(n)的共轭对称部分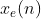 的FT是
的FT是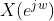 的实部
的实部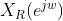 ;序列x(n)的共轭反对称部分
;序列x(n)的共轭反对称部分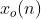 的FT是
的FT是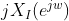 ,即:
,即:
证明:
同理可得:
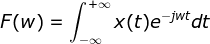
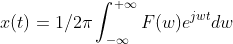
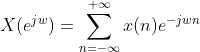
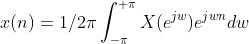

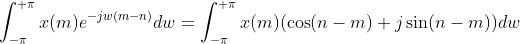
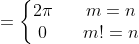
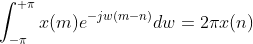
![FT[x(n-n_{0})]=X(e^{^{jw}})e^{-jwn_{0}}](https://images2.imgbox.com/a7/7a/AQngJONu_o.gif)
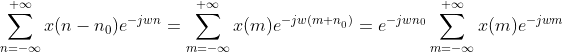
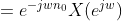
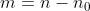
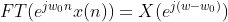
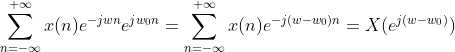
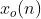
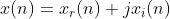
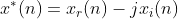
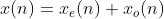
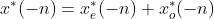
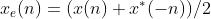
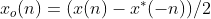
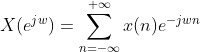
![\sum_{n=-\infty }^{+\infty }x^{*}(-n)e^{-jwn}=[\sum_{n=-\infty }^{+\infty }x(-n)e^{jwn}]^{*}=[\sum_{m=+\infty }^{-\infty }x(m)e^{-jwm}]^{*}=X^{*}(e^{jw})](https://images2.imgbox.com/82/8d/zfjPlpbn_o.gif)
![\sum_{n=-\infty }^{+\infty }x^{*}(n)e^{-jwn}=[\sum_{n=-\infty }^{+\infty }x(n)e^{jwn}]^{*}=[\sum_{n=-\infty }^{+\infty }x(n)e^{-j(-w)n}]^{*}=X^{*}(e^{-jw})](https://images2.imgbox.com/0a/6c/d5MAGHhK_o.gif)
![FT[x_{r}(n)]=X_{e}(e^{jw})=X_{e}^{*}(e^{-jw})](https://images2.imgbox.com/df/c8/oclegpjs_o.gif)
![FT[jx_{i}(n)]=X_{o}(e^{jw})=-X_{o}^{*}(e^{-jw})](https://images2.imgbox.com/65/09/fsJ6TGEW_o.gif)
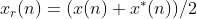
![FT[x_{_{r}}(n)]=[X(e^{jw})+X^{*}(e^{-jw})]/2=X_{e}(e^{jw})](https://images2.imgbox.com/2c/ff/aaXbycdB_o.gif)
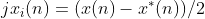
![FT[jx_{_{i}}(n)]=[X(e^{jw})-X^{*}(e^{-jw})]/2=X_{o}(e^{jw})](https://images2.imgbox.com/cb/b6/6E0OEV8g_o.gif)
![FT[x_{e}(n)]=X_{R}(e^{jw})](https://images2.imgbox.com/33/61/TZB3qhIA_o.gif)
![FT[x_{o}(n)]=jX_{I}(e^{jw})](https://images2.imgbox.com/03/dc/e4CdZL1w_o.gif)
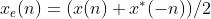
![FT[x_{_{e}}(n)]=[X(e^{jw})+X^{*}(e^{jw})]/2=X_{R}(e^{jw})](https://images2.imgbox.com/05/60/pGCR271U_o.gif)
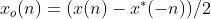
![FT[x_{_{o}}(n)]=[X(e^{jw})-X^{*}(e^{jw})]/2=jX_{I}(e^{jw})](https://images2.imgbox.com/28/4d/pvqATCRr_o.gif)