Codeforces 1374 E2. Reading Books (hard version) —— 想法，贪心

This way

题意：

现在有两个人要一起读书，有n本书，他们要读正好m本，每本书有3个属性：
t：表示读完这本书要的时间，a：第一个人是否喜欢这本书，b：第二个人是否喜欢这本书。
让你构造一种方案使得他们读的书正好是m本，并且这些书中第一个人喜欢的书有>=k本，第二个人喜欢的书有>=k本，并且读书时间最少。

题解：

感觉最近做的题目都有点贪心的思想。并且这道题目 恶心到我了，我做了很久，一开始的想法错误到后来改正了想法之后慢慢debug。
但是这道题目就听听思路就好了，我的代码的话有点长，可能看完之后在重新想一遍会来的舒服一点。
但是时间复杂度还算可以，就一个排序是$O(nlogn)$，其它是$O(n)$的

那么首先可以知道，一旦(1,1)的数量定了，那么我们可以通过贪心的方法去做，也就是答案就定了。
那么我们如何在枚举(1,1)的数量的同时快速的得到答案？
假设我当前有这么多的(1,1)，这么多的(0,1)，还有这么多的(1,0)和(0,0)

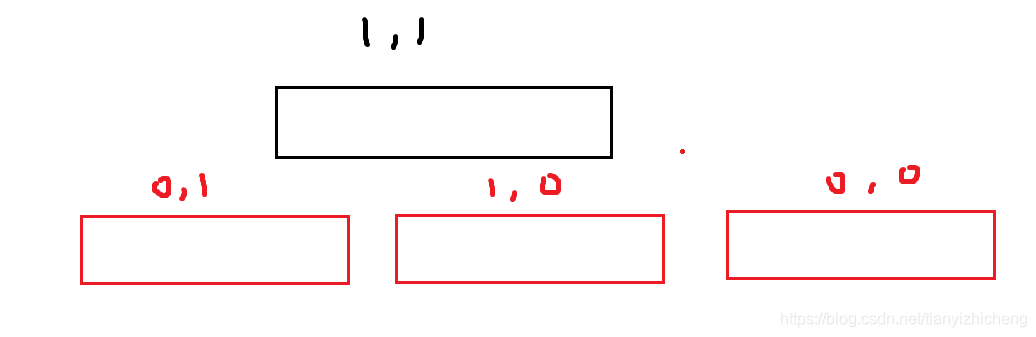
我如果这些都是排好序的，那么我新增一个(1,1)的时候，是不是只需要将下面3中情况的末尾拿掉，然后再放进去三种情况中可以选择的两个最大的进去就好了？

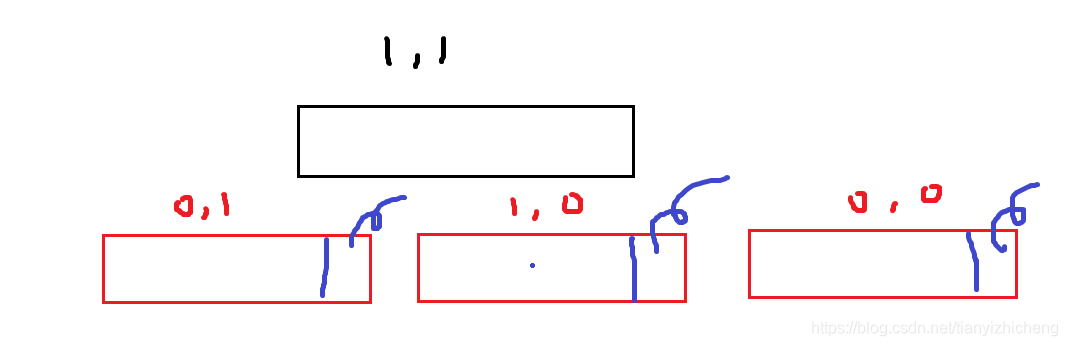
那么方法就很明显了：
我这里使用的是双端队列，因为一旦一开始排序之后，每本书的相对位置就不会改变。
我用s表示当前在答案里的书，rt表示当前可以选择的书。
那么首先考虑的是是否能在m本书之内让每个人都得到k本喜欢的书。
然后的话

while(s[3].size()+min(mi,(m-(int)s[3].size())/2)<k||s[3].size()+rt[1].size()+rt[2].size()+rt[0].size()<m)

这个表示最少需要放的(1,1)的个数
再然后，我们就像刚才所说的，新增(1,1)的时候把下面三种的末尾抛掉，再塞两个进来。注意一些细节，我这里就不赘述了

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
struct node{
    int tim,a,b,id;
    bool operator< (const node& aa)const {
        return tim<aa.tim;
    }
}a[N];
deque<node>s[5],rt[5];
int vis[N];
vector<int>ad,de;
int main()
{
    int n,m,k;
    scanf("%d%d%d",&n,&m,&k);
    for(int i=1;i<=n;i++)
        scanf("%d%d%d",&a[i].tim,&a[i].a,&a[i].b),a[i].id=i;
    sort(a+1,a+1+n);
    int na=0,nb=0,ans=2e9;
    for(int i=1;i<=n;i++){
        int ne=0;
        if(a[i].a)ne|=1;
        if(a[i].b)ne|=2;
        rt[ne].push_back(a[i]);
    }
    int sum=0;
    int x=(int)rt[1].size(),y=(int)rt[2].size();
    int mi=min(x,y);
    if((int)rt[3].size()+min(mi,(m-(int)rt[3].size())/2)<k)return 0*printf("-1\n");
    
    while(s[3].size()+min(mi,(m-(int)s[3].size())/2)<k||s[3].size()+rt[1].size()+rt[2].size()+rt[0].size()<m){
        s[3].push_back(rt[3].front());
        sum+=rt[3].front().tim;
        vis[rt[3].front().id]=1;
        rt[3].pop_front();
    }
    int ned=k-s[3].size();
    for(int i=1;i<=ned;i++){
        s[2].push_back(rt[2].front());
        sum+=rt[2].front().tim;
        vis[rt[2].front().id]=1;
        rt[2].pop_front();
        s[1].push_back(rt[1].front());
        sum+=rt[1].front().tim;
        vis[rt[1].front().id]=1;
        rt[1].pop_front();
    }
    int res=m-s[3].size()-max(0,2*(k-(int)s[3].size()));
    for(int i=1;i<=res;i++){
        int add=-1;
        if(rt[0].size())
            add=0;
        if(rt[1].size()&&(add==-1||rt[add].front().tim>rt[1].front().tim))
            add=1;
        if(rt[2].size()&&(add==-1||rt[add].front().tim>rt[2].front().tim))
            add=2;
        s[add].push_back(rt[add].front());
        sum+=rt[add].front().tim;
        vis[rt[add].front().id]=1;
        rt[add].pop_front();
    }
    ans=sum;
    
    for(;rt[3].size()&&s[3].size()<m;){
        sum=ans;
        ad.clear(),de.clear();
        s[3].push_back(rt[3].front());
        ad.push_back(rt[3].front().id);
        sum+=rt[3].front().tim;
        rt[3].pop_front();
        int num=0;
        if(s[2].size()){
            rt[2].push_front(s[2].back());
            de.push_back(s[2].back().id);
            sum-=s[2].back().tim;
            s[2].pop_back();
            num++;
        }
        if(s[1].size()){
            rt[1].push_front(s[1].back());
            de.push_back(s[1].back().id);
            sum-=s[1].back().tim;
            s[1].pop_back();
            num++;
        }
        if(s[0].size()){
            rt[0].push_front(s[0].back());
            de.push_back(s[0].back().id);
            sum-=s[0].back().tim;
            s[0].pop_back();
            num++;
        }
        while(num>1){
            int add=-1;
            if(rt[0].size())
                add=0;
            if(rt[1].size()&&(add==-1||rt[add].front().tim>rt[1].front().tim))
                add=1;
            if(rt[2].size()&&(add==-1||rt[add].front().tim>rt[2].front().tim))
                add=2;
            s[add].push_back(rt[add].front());
            sum+=rt[add].front().tim;
            ad.push_back(rt[add].front().id);
            rt[add].pop_front();
            num--;
        }
        if(sum<ans){
            for(int i:ad)
                vis[i]++;
            for(int i:de)
                vis[i]--;
            ans=sum;
        }
    }
    printf("%d\n",ans);
    for(int i=1;i<=n;i++)
        if(vis[i])
            printf("%d ",i);
    printf("\n");
    return 0;
}