极大似然估计方法(Maximum Likelihood Estimate Method)
定义
极大似然估计方法(Maximum Likelihood Estimate,MLE)也称最大概似估计或最大似然估计: 利用已知的样本结果,反推最有可能(最大概率)导致这样的结果的参数值。
思想:已经拿到很多个样本,这些样本值已实现,最大似然估计就是找参数估计值,使得前面已经实现的样本值发生概率最大。
本质:其是一种概率论在统计学的应用,是参数估计的方法之一;其是一种粗略的数学期望,要知道它的误差大小还要做区间估计。
#针对情况
针对一些情况:样本太多,无法得出分布的参数值,可以通过采样小样本后,利用极大似然估计方法获取假设中分布的参数值。
步骤
(1)写出似然函数:
总体为离散型时:

总体为连续型时:
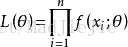
(2)对似然函数两边取对数
总体为离散型时:

总体为连续型时:

(3)对lnL(θ)求导数并令之为0,求出未知参数的最大似然估计值(极值):
注:一阶的微分和可导可近似;取ln是因为对数比较方便求导。
#例子
例一
一个麻袋里面有白球和黑球,不知道它们之间的数量比例,有放回的抽取10次,结果为:8次黑球和2次白球,我需求最有可能的黑白球之间的比例,这时候可采取最大似然估计法。
很多人马上有了答案:80%,其背后的理论支撑是什么?
设:抽到黑球的概率为p,则白球的概率为1-p。因为每次抽出求的颜色都服从独立分布。
我们把每次抽出来球的颜色为一次抽样,则黑球事件的概率为P(样本结果|Model)。
记第一次抽样的结果为x1,则第n次为xn.
得出8次黑球和2次白球的结果概率:
以上就为概率表达式,而我们要求的模型的参数,就是求p。
有无数的p供我们选择,极大似然估计采取的选择原则是让这个样本结果出现的可能性最大,就是使上述概率表达式最大。将p看成方程求极值即可,即求导的过程就是求极值的过程.
最后求得P=80%.
例二
假如噪声服从正态分布,但该分布的均值与方差未知。选取大量的噪声作为我们观察样本结果,然后通过最大似然估计来获取上述假设的正太分布的参数,即可知道正态分布的期望和方差。
也就是说通过小样本的采样就知道一系列重要的数学指标量。