输出层的激活函数——softmax函数
概括
机器学习的问题大致可以分为分类问题和回归问题。分类问题是数据属于哪一个类别的问题。比如,区分图像中的人是男性还是女性的问题就是分类问题。而回归问题是根据某个输入预测一个(连续的)数值的问题。比如,根据一个人的图像预测这个人的体重问题是回归问题(类似“57.4kg”这样的预测)。
输出层所用的激活函数,根据求解问题的性质决定。一般,回归问题可以用恒等函数,二元分类问题可以用sigmoid函数,多元分类问题可以用softmax函数。
恒等函数:输出=输入
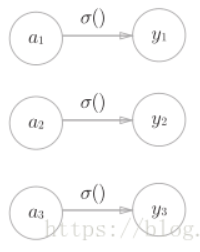
softmax函数:输出为一个函数
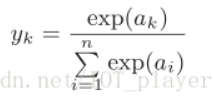
其中exp为指数函数,表示假设输出层共有n个神经元,计算第k个神经元的输出yk。ak代表第k个输出神经元的输入,ai代表第i个输出神经元的输入,公式分子表示ak的指数函数,分母表示所有输出神经元的输入指数函数的和
代码实现softmax
def softmax(a):
exp_a = np.exp(a)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
softmax函数的注意事项
上述softmax函数的实现存在溢出问题。在计算指数时,比如e的5000次方,数据将会非常大,计算机处理“数”时,数值必须在4字节或8字节的有限数据宽度内,超出的数据则会显示为无穷(inf),所以要对softmax函数进行改进,防止数据的溢出。
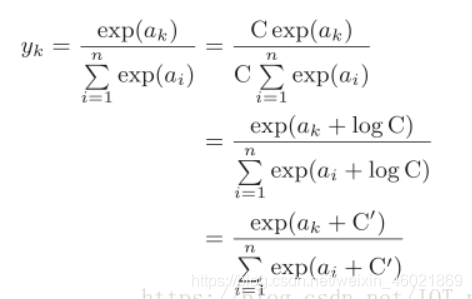
如图中,将分子分母同时乘以C,然后将C提进指数函数中,图中用的logC理解成数学中的lnC,然后用C’代替logC,通过控制C’来控制exp函数中的指数,来实现softmax函数不因为数据过大而出错。C’可以使用任何值,为防止溢出,一般使用输入信号中的最大值。
例子:
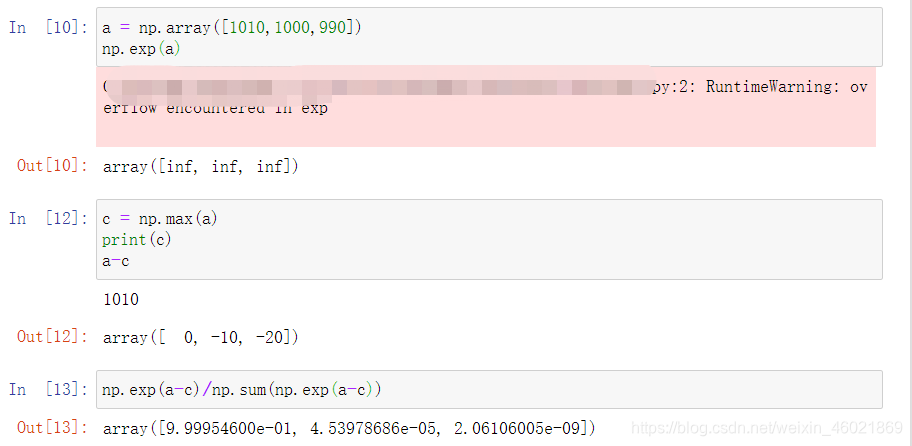
def softmax(a):
c = np.max(a)
exp_a = np.exp(a-c) # 溢出对策
sum_exp_a = np.sum(exp_a)
y = exp_a/sum_exp_a
return y