动手学机器学习(第二版) 第三章分类
第三章 分类
import numpy as np
本章使用MNIST数据集,该数据集包含70,000张由美国的高中生和人口调查局手写数字的图像,使用Scikit-Learn提供的函数可以很方便第下载这些数据集
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', version=1)
mnist.keys()
dict_keys(['data', 'target', 'frame', 'categories', 'feature_names', 'target_names', 'DESCR', 'details', 'url'])
由Scikit-Learn下载的数据集通常有相似的数据结构:
DESCR: 描述数据集的基本信息data: 每个实例用一行数组表示,每列表示一个特征target: 包含标签的数组
X, y = mnist["data"], mnist["target"]
X.shape
(70000, 784)
y.shape
(70000,)
总共有70,000张图片,每张图片有784个特征。这是因为每一张图片是
28
×
28
28\times28
28×28 的分辨率,每个特征简单的代表像素点的强度,从0(白)到255(黑)。查看数据集中的手写数字,只需要选择实例的一个特征向量,然后将其重新变为
28
×
28
28\times28
28×28 的数组,再用Matplotlib’s imshow()函数画图显示
import matplotlib as mpl
import matplotlib.pyplot as plt
import random
# 随机选择一张图片
# random_ind = random.randint(0,7e4)
random_ind = 0
print("chose No.",random_ind," pic; label: ", y[random_ind])
some_digit = X[random_ind]
some_digit_image = some_digit.reshape(28, 28)
plt.imshow(some_digit_image, cmap=mpl.cm.binary, interpolation="nearest")
plt.axis("off")
plt.show()
chose No. 0 pic; label: 5
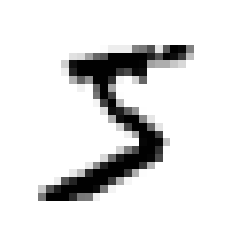
# 查看label标记,发现其格式是字符串
y[random_ind]
'5'
# 将字符串label转换为整型数组
y = y.astype(np.uint8)
在训练之前,一般需要将数据集分为训练数据和测试数据,MNIST数据集已经帮我们分好了训练数据集(前60,000张图片)和测试数据集(后10,000张图片)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
训练数据集的顺序已经打乱,这保证了所有的交叉验证是一致的(你也不想一折交叉验证缺少一些数字的图片). 另外,一些学习算法对训练实例的输入顺序敏感,在许多同样的实例在一行输入时,这些算法表现的很差. 打乱数据集的顺序保证了这些不会发生
训练二元分类器
我们来简化问题,仅辨认一个数字,例如数字5. “5”分类器是一个二元分类器的例子,能够分辨为两类,5和非5.
y_train_5 = (y_train == y[random_ind])
y_test_5 = (y_test == y[random_ind])
然后我们选择一个分类器来训练. 一个方法是选择随机梯度下降(Stochastic Gradient Descent, SGD)分类器,使用Scikit-Learns SGDClassifier`类. 这个类的优点是可以高效地处理大量的数据. 这是因为SGD算法可以每次单独训练一个输入实例,这也让SDG适合实时学习.
from sklearn.linear_model import SGDClassifier
sgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(X_train, y_train_5)
SGDClassifier(random_state=42)
# 使用训练的SDG模型预测数字5
sgd_clf.predict([some_digit])
array([ True])
性能评估
评价分类器的性能常常比评价回归的性能更具有欺骗性,所以需要花费很大的精力研究分类器的评估
使用交叉验证评估准确率
实施交叉验证
手动实现交叉验证,代码如下所示. StratifiedFold方法实现了分层采样,每次迭代都创建了分类器的副本,在副本上训练训练样本,然后在测试样本上预测,最后比较正确预测并输出正确率
from sklearn.model_selection import StratifiedKFold
from sklearn.base import clone
skfolds = StratifiedKFold(n_splits=3, random_state=42)
for train_index, test_index in skfolds.split(X_train, y_train_5):
clone_clf = clone(sgd_clf)
X_train_folds = X_train[train_index]
y_train_folds = y_train_5[train_index]
X_test_fold = X_train[test_index]
y_test_fold = y_train_5[test_index]
clone_clf.fit(X_train_folds, y_train_folds)
y_pred = clone_clf.predict(X_test_fold)
n_correct = sum(y_pred == y_test_fold)
print(n_correct / len(y_pred))
0.95035
0.96035
0.9604
# 使用cross_val_score()测试分类
from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")
array([0.95035, 0.96035, 0.9604 ])
以上交叉验证的准确率都在93%以上,看起来效果十分好. 但是再这之前,设置一个很傻的分类器,将每张图片都设置为非5类
from sklearn.base import BaseEstimator
class Never5Classifier(BaseEstimator):
def fit(self, X, y=None):
pass
def predict(self, X):
return np.zeros((len(X),1), dtype=bool)
never_5_clf = Never5Classifier()
cross_val_score(never_5_clf, X_train,y_train_5, cv=3, scoring="accuracy")
array([0.91125, 0.90855, 0.90915])
可以看到,这个很傻的分类器也有90%以上的准确率,这是因为数据集中只有10%左右的图片是5,所以一直猜测图片不是5,你也能得到90%的准确率
这表明了为什么准确率通常不是衡量分类器的最好方法,特别是在处理有数据倾斜的情况下(例如,当一些类别的数据比其他类别的数据出现地更加频繁)
混淆矩阵(Confusion Matrix)
from sklearn.model_selection import cross_val_predict
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
from sklearn.metrics import confusion_matrix
confusion_matrix(y_train_5, y_train_pred)
array([[53892, 687],
[ 1891, 3530]])
在混淆矩阵中的每一行代表实际的类别,每一列代表预测的类列。
- 数组的第一行是被实际非5的图片(负类), 53,892张图片被正确地分类为非5(True Negative,TN),剩余有687张图片错分为5(False Positive, FP)
- 第二行是实际为5的图片(正类),1,891张图片被错误分为非5(False Negative, FN),而剩下的3,530张图片是正确分为5的图片(True Positive, TP)
一个完美的分类器只有真负类(TN)和真正类(TP),所以混淆矩阵只能在主对角线有非零值,如下所示
y_train_perfect_predictions = y_train_5
confusion_matrix(y_train_5, y_train_perfect_predictions)
array([[54579, 0],
[ 0, 5421]])
混淆矩阵告诉了你很多信息,但是有时你可能更想要更多准确的度量标准。一种方法是检查正类的准确率,这被称作分类器的准确率
p r e c i s i o n = T P T P + F P precision = \frac{TP}{TP+FP} precision=TP+FPTP
一个很简单地获得完美精度的方法是只做正类预测(precison=1/1=100%),分类器会忽略其他的类别,除了正类的实例,这种度量方法就会失效,所以精确率一般和另一种度量方法同时使用,叫做召回率(recall),同样也叫做敏感度或者真正率
r e c a l l = T P T P + F N recall = \frac{TP}{TP+FN} recall=TP+FNTP
准确率和召回率
from sklearn.metrics import precision_score, recall_score
precision_score(y_train_5, y_train_pred)
0.8370879772350012
recall_score(y_train_5, y_train_pred)
0.6511713705958311
结合准确率和召回率的简单方法是F1分数,它是准确率和召回率的调和平均数
F 1 = 2 1 p r e c i s i o n + 1 r e c a l l = 2 × p r e c i s i o n × r e c a l l p r e c i s i o n + r e c a l l = T P T P + F N + F P 2 F_1 =\frac{2}{\frac{1}{precision} + \frac{1}{recall}} = 2 \times \frac{precision \times recall}{precision + recall} = \frac{TP}{TP+\frac{FN+FP}{2}} F1=precision1+recall12=2×precision+recallprecision×recall=TP+2FN+FPTP
只有在召回率和准确率都同时高, F 1 F_1 F1 才会高,但是一般情况下,两者是此消彼长的关系,这叫做准确率和召回率折中(precison/recall tradeoff)
from sklearn.metrics import f1_score
f1_score(y_train_5, y_train_pred)
0.7325171197343846
准确率/回调率折中
y_scores = sgd_clf.decision_function([some_digit])
y_scores
array([2164.22030239])
threshold = 0
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred
array([ True])
threshold = 8000
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred
array([False])
y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function")
y_scores
array([ 1200.93051237, -26883.79202424, -33072.03475406, ...,
13272.12718981, -7258.47203373, -16877.50840447])
from sklearn.metrics import precision_recall_curve
precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)
def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
plt.plot(thresholds, precisions[:-1], "b--", label="Precision")
plt.plot(thresholds, recalls[:-1], "g-", label="Recall")
plt.grid()
plt.legend(["Precision", "Recall"])
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.show()
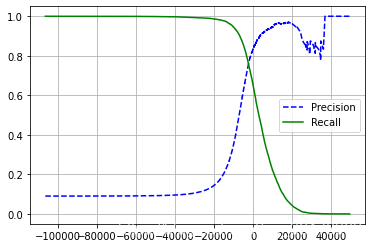
plt.plot(recalls,precisions)
plt.grid()
plt.xlim(0, 1)
plt.ylim(0, 1)
plt.show()
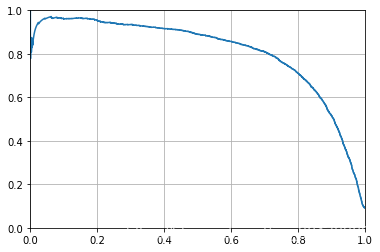
如果决定获取90%准确率,查看准确率和召回率的图片,可以找到阈值,更精确的是找到最低能使模型达到90%准确率的阈值
threshold_90_precision = thresholds[np.argmax(precisions >= 0.90)]
threshold_90_precision
3370.0194991439557
y_train_pred_90 = (y_scores >= threshold_90_precision)
y_train_pred_90
array([False, False, False, ..., True, False, False])
precision_score(y_train_5, y_train_pred_90)
0.9000345901072293
recall_score(y_train_5, y_train_pred_90)
0.4799852425751706
The ROC Curve
观察者操作特性曲线(receiver operating characteristic, ROC)是另一种常用于二分类器的工具. 它和准确率/召回率曲线类似,但是ROC曲线绘制的是真正率(TPR,回调的另一种说法)和假正类(FPR)的比值。
from sklearn.metrics import roc_curve
fpr, tpr, threshold = roc_curve(y_train_5, y_scores)
def plot_roc_curve(fpt, tpr, label=None):
plt.plot(fpr, tpr, linewidth=2, label=label)
plt.plot([0, 1],[0, 1], 'k--')
plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate(Recall)")
plot_roc_curve(fpr, tpr)
plt.show()
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HsKuD9HJ-1595927822631)(chap3_files/chap3_53_0.svg)]](https://images2.imgbox.com/38/72/3GaVLerS_o.png)
同样地,这里也有平衡的关系,回调(recall, or TPR)越高,分类器产生的假正率越高。点线代表的是完全随机的分类器的ROC曲线;一个好的分类器离这条线越远越好(趋向于左上角)
另外一种比较分类器的方法是测量曲线下的面积(area under the curve, AUC). 完美的分类器ROC AUC等于一,而完全随机的分类器的ROC AUC等于0.5. Scikit-Learn提供了一个计算ROC AUC的函数.
from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5, y_scores)
0.9604938554008616
当正类较少时,使用PR曲线,反之则是ROC曲线
训练一个RandomForestClassifier并与SGDClassifier比较ROC曲线和ROC AUC分数
from sklearn.ensemble import RandomForestClassifier
forest_clf = RandomForestClassifier(random_state=42)
y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3, method="predict_proba")
y_scores_forest = y_probas_forest[:, 1]
fpr_forest, tpr_forest, thresholds_forest = roc_curve(y_train_5, y_scores_forest)
plt.plot(fpr, tpr, "b:", label="SGD")
plt.plot(fpr_forest, tpr_forest, label="Random Forest")
plt.legend(loc="lower right")
plt.xlim((-0.01,1))
plt.ylim((0,1))
plt.show()
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ADUVci67-1595927822632)(chap3_files/chap3_60_0.svg)]](https://images2.imgbox.com/ed/35/1xCJMFKy_o.png)
# 该代码出现未知错误。。。
# roc_auc_score(y_train, y_scores_forest)
多元分类
相比于二元分类器只能分辨两类,多元分类器(multiclass classifiers, also called multinomial classifiers)可以分辨超过两类.
一些算法(例如随机森林分类器或者朴素贝叶斯分类器)可以直接处理多分类问题,其他的算法(例如支持向量机或者线性分类器)只能作二分类器.但也有一些策略让你可以用多个二分类器来实现多元分类器
- 用多个二分类器,每个分类器判断一类,对于每个实例,判断所有分类器输出的最高的得分,这叫做one-versus-all(OvA)策略,也叫作one-versus-the-rest
- 训练关于每一对数字的二分类器,例如分辨0和1,这种策略叫做one-versus-one(OvO)。如果有 N N N 个分类,那么需要训练 N × ( N − 1 ) 2 \frac{N \times (N-1)}{2} 2N×(N−1) 个分类器
一些算法(例如支持向量机)和训练集的大小关系不大,所以对于这些算法OvO更加合适,因为它可以在小规模的数据集上训练很多的分类器,而不是在很大的数据集上训练很少的分类器。但是对于大多数的二分类算法来说,OvA更适用
sgd_clf.fit(X_train, y_train)
sgd_clf.predict([some_digit])
array([3], dtype=uint8)
Scikit-Learn检测到你使用二分类算法进行多元分类任务时,它会自动运行OvA(除了SVM会自动运行OvO)。
some_digit_scores = sgd_clf.decision_function([some_digit])
some_digit_scores
array([[-31893.03095419, -34419.69069632, -9530.63950739,
1823.73154031, -22320.14822878, -1385.80478895,
-26188.91070951, -16147.51323997, -4604.35491274,
-12050.767298 ]])
np.argmax(some_digit_scores)
3
sgd_clf.classes_
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=uint8)
分类器训练好之后,在其
classes_属性储存目标类的列表
强制ScikitLearn使用one-versus-one或者one-versus-all,可以使用OneVsOneClassifier或者OneVsRestClassifier
from sklearn.multiclass import OneVsOneClassifier
ovo_clf = OneVsOneClassifier(SGDClassifier(random_state=42))
ovo_clf.fit(X_train, y_train)
ovo_clf.predict([some_digit])
array([5], dtype=uint8)
len(ovo_clf.estimators_)
45
forest_clf.fit(X_train, y_train)
RandomForestClassifier(random_state=42)
forest_clf.predict([some_digit])
array([5], dtype=uint8)
forest_clf.predict_proba([some_digit])
array([[0. , 0. , 0.01, 0.08, 0. , 0.9 , 0. , 0. , 0. , 0.01]])
cross_val_score(sgd_clf, X_train, y_train, cv=3, scoring="accuracy")
array([0.87365, 0.85835, 0.8689 ])
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train.astype(np.float64))
cross_val_score(sgd_clf, X_train_scaled, y_train,cv=3,scoring="accuracy")
array([0.8983, 0.891 , 0.9018])
误差分析
y_train_pred = cross_val_predict(sgd_clf, X_train_scaled, y_train, cv=3)
conf_mx = confusion_matrix(y_train, y_train_pred)
conf_mx
array([[5577, 0, 22, 5, 8, 43, 36, 6, 225, 1],
[ 0, 6400, 37, 24, 4, 44, 4, 7, 212, 10],
[ 27, 27, 5220, 92, 73, 27, 67, 36, 378, 11],
[ 22, 17, 117, 5227, 2, 203, 27, 40, 403, 73],
[ 12, 14, 41, 9, 5182, 12, 34, 27, 347, 164],
[ 27, 15, 30, 168, 53, 4444, 75, 14, 535, 60],
[ 30, 15, 42, 3, 44, 97, 5552, 3, 131, 1],
[ 21, 10, 51, 30, 49, 12, 3, 5684, 195, 210],
[ 17, 63, 48, 86, 3, 126, 25, 10, 5429, 44],
[ 25, 18, 30, 64, 118, 36, 1, 179, 371, 5107]])
plt.matshow(conf_mx, cmap=plt.cm.gray)
plt.show()
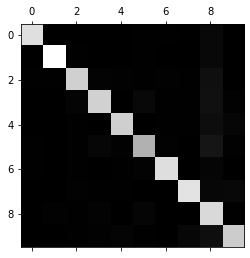
误差矩阵看起来很好,大多数的图片在主对角线上,这意味着分类正确。
row_sums = conf_mx.sum(axis=1, keepdims=True)
norm_conf_mx = conf_mx / row_sums
np.fill_diagonal(norm_conf_mx, 0)
plt.matshow(norm_conf_mx, cmap=plt.cm.gray)
plt.show()
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5SrV3097-1595927822635)(chap3_files/chap3_81_0.svg)]](https://images2.imgbox.com/dc/73/aRWfHpEW_o.png)
将对角线置0,观察误差,发现第8行最明显
# EXTRA
def plot_digits(instances, images_per_row=10, **options):
size = 28
images_per_row = min(len(instances), images_per_row)
images = [instance.reshape(size,size) for instance in instances]
n_rows = (len(instances) - 1) // images_per_row + 1
row_images = []
n_empty = n_rows * images_per_row - len(instances)
images.append(np.zeros((size, size * n_empty)))
for row in range(n_rows):
rimages = images[row * images_per_row : (row + 1) * images_per_row]
row_images.append(np.concatenate(rimages, axis=1))
image = np.concatenate(row_images, axis=0)
plt.imshow(image, cmap = mpl.cm.binary, **options)
plt.axis("off")
cl_a, cl_b = 3, 5
X_aa = X_train[(y_train == cl_a) & (y_train_pred == cl_a)]
X_ab = X_train[(y_train == cl_a) & (y_train_pred == cl_b)]
X_ba = X_train[(y_train == cl_b) & (y_train_pred == cl_a)]
X_bb = X_train[(y_train == cl_b) & (y_train_pred == cl_b)]
plt.figure(figsize=(8,8))
plt.subplot(221); plot_digits(X_aa[:25], images_per_row=5)
plt.subplot(222); plot_digits(X_ab[:25], images_per_row=5)
plt.subplot(223); plot_digits(X_ba[:25], images_per_row=5)
plt.subplot(224); plot_digits(X_bb[:25], images_per_row=5)
plt.show()
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-buhm99FE-1595927822636)(chap3_files/chap3_84_0.svg)]](https://images2.imgbox.com/0f/34/7GYNj9lP_o.png)
多标签分类
目前对于每个实例只能分配一个类,但是在一些例子中或许需要输出多个分类,比如一张图片中有多个人,可以用一个矩阵表示,例如[1,0,1],表示第一个类和第三个类存在
from sklearn.neighbors import KNeighborsClassifier
y_train_large = (y_train >= 7)
y_train_odd = (y_train % 2 == 1)
y_multilabel = np.c_[y_train_large, y_train_odd]
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_multilabel)
KNeighborsClassifier()
knn_clf.predict([some_digit])
array([[False, True]])
y_multilabel包含两个标签:第一个是>=7,第二个是判断是否奇数,训练后预测5,结果显示5>=7为False,而5%2==1为True
# 这段代码运行慢的吐血!!!
# y_train_knn_pred = cross_val_predict(knn_clf, X_train, y_multilabel, cv=3)
# f1_score(y_multilabel, y_train_knn_pred, average="macro")
多输出分类
多输出分类简单的来说就是综合多分类输出,其中每个样本可以是多个种类
noise = np.random.randint(0, 100, (len(X_train), 784))
X_train_mod = X_train + noise
noise = np.random.randint(0,100, (len(X_test), 784))
X_test_mod = X_test + noise
y_train_mod = X_train
y_test_mod = X_test
# 查看添加噪声后的图片
plt.subplot(121)
plt.imshow(X_train_mod[0].reshape(28, 28), cmap = mpl.cm.binary)
plt.axis("off")
plt.subplot(122)
plt.imshow(y_train_mod[0].reshape(28, 28), cmap = mpl.cm.binary)
plt.axis("off")
plt.show()
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AvAC12am-1595927822636)(chap3_files/chap3_92_0.svg)]](https://images2.imgbox.com/85/67/VRGK3wJS_o.png)
knn_clf.fit(X_train_mod, y_train_mod)
some_index = 0
clean_digit = knn_clf.predict([X_test_mod[some_index]])
plot_digits(clean_digit)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PqQNRchu-1595927822637)(chap3_files/chap3_94_0.svg)]](https://images2.imgbox.com/d0/d8/N6Cc8Mtd_o.png)